Memory Consumption
Optimizing Memory Consumption in Deep Learning
Over the last ten years, a constant trend in deep learning is towards deeper and larger networks. Despite rapid advances in hardware performance, cutting-edge deep learning models continue to push the limits of GPU RAM. So even today, it’s always desirable to find ways to train larger models while consuming less memory. Doing so enables us to train faster, using larger batch sizes, and consequently achieving a higher GPU utilization rate.
In this document, we explore techniques for optimizing memory allocation for deep neural networks. We discuss a few candidate solutions. While our proposals are by no means exhaustive, these solutions are instructive and allow us to introduce the major design issues at play.
Computation Graph
First, let’s revisit the idea of the computation graph. A computation graph describes the (data flow) dependencies between the operations in the deep network. The operations performed in the graph can be either fine-grained or coarse-grained. The following figure shows two examples of computation graphs.
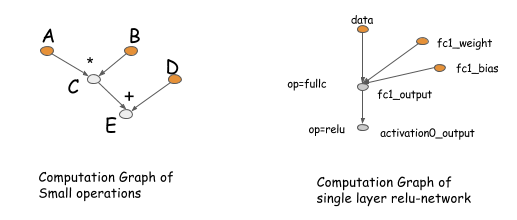
The concept of a computation graph is explicitly encoded in packages like Theano and CGT. In other libraries, computation graphs appear implicitly as network configuration files. The major difference in these libraries comes down to how they calculate gradients. There are mainly two ways: performing back-propagation on the same graph or explicitly representing a backwards path to calculate the required gradients.
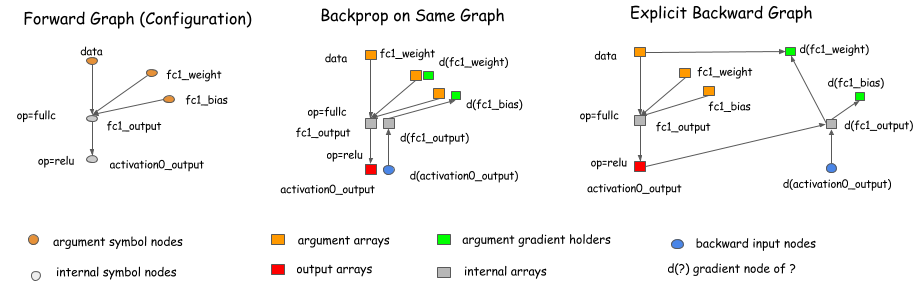
Libraries like Caffe, CXXNet, and Torch take the former approach, performing back-prop on the original graph. Libraries like Theano and CGT take the latter approach, explicitly representing the backward path. In this discussion, we adopt the explicit backward path approach because it has several advantages for optimization.
However, we should emphasize that choosing the explicit backward path approach doesn’t restrict us
to symbolic libraries, such as Theano and CGT. We can also use the explicit backward path for gradient calculation of
layer-based (which ties forward and backward together) libraries. The following graph shows how to do this.
Basically, we introduce a backward node that links to the forward node of the graph and calls the layer.backward
in the backward operations.
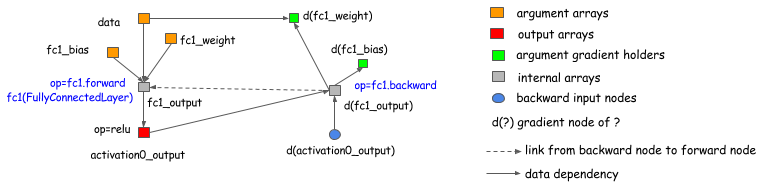
This discussion applies to almost all existing deep learning libraries. (There are differences between libraries, e.g., higher-order differentiation, which is beyond the scope of this topic.)
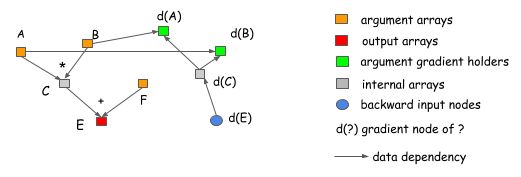
Why is the explicit backward path better? Let’s explain it with two examples.
The first reason is that the explicit backward path
clearly describes the dependency between computations.
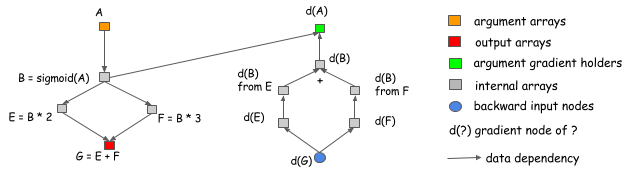
Consider the following case, where we want to get
the gradient of A and B. As we can see clearly from the graph,
the computation of the d(C) gradient doesn’t depend on F.
This means that we can free the memory of F
right after the forward computation is done.
Similarly, the memory of C can be recycled.
Another advantage of the explicit backward path is the ability to have a different backward path, instead of a mirror of forward one. A common example is the split connection case, as shown in the following figure.
In this example, the output of B is referenced by two operations. If we want to do the gradient calculation in the same network, we need to introduce an explicit split layer. This means we need to do the split for the forward pass, too. In this figure, the forward pass doesn’t contain a split layer, but the graph will automatically insert a gradient aggregation node before passing the gradient back to B. This helps us to save the memory cost of allocating the output of the split layer, and the operation cost of replicating the data in the forward pass.
If we adopt the explicit backward approach, there’s no difference between the forward pass and the backward pass. We simply step through the computation graph in chronological order and carry out computations. This makes the explicit backward approach easy to analyze. We just need to answer the question: how do we allocate memory for each output node of a computation graph?
What Can Be Optimized?
As you can see, the computation graph is a useful way to discuss memory allocation optimization techniques. Already, we’ve shown how you can save some memory by using the explicit backward graph. Now let’s explore further optimizations, and see how we might determine reasonable baselines for benchmarking.
Assume that we want to build a neural network with n layers.
Typically, when implementing a neural network,
we need to allocate node space for both the output of each layer
and the gradient values used during back-propagation.
This means we need roughly 2 n memory cells.
We face the same requirement when using the explicit backward graph approach
because the number of nodes in a backward pass
is roughly the same as in a forward pass.
In-place Operations
One of the simplest techniques we can employ is in-place memory sharing across operations. For neural networks, we can usually apply this technique for the operations corresponding to activation functions. Consider the following case, where we want to compute the value of three chained sigmoid functions.
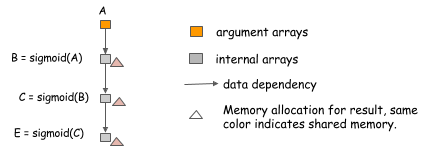
Because we can compute sigmoid in-place,
using the same memory for input and output,
we can compute an arbitrary-length chain
of sigmoid functions using constant memory.
Note: it’s easy to make mistakes when implementing in-place optimization. Consider the following case, where the value of B is used not only by C, but also by F.
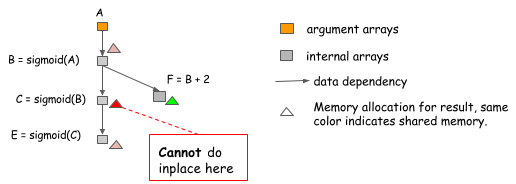
We can’t perform in-place optimization because the value of B
is still needed after C=sigmoid(B) is computed.
An algorithm that simply does in-place optimization
for every sigmoid operation might fall into such trap,
so we need to be careful about when we can use it.
Standard Memory Sharing
In-place operations are not the only places where we can share memory. In the following example, because the value of B is no longer needed after we compute E, we can reuse B’s memory to hold the result of E.
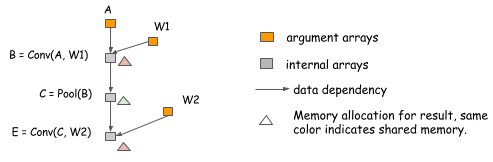
Memory sharing doesn’t necessarily require the same data shape.
Note that in the preceding example, the shapes of B and E can differ.
To handle such a situation, we can allocate a memory region
of size equal to the maximum of that required by B and E and share it between them.
Example of Real Neural Network Allocation
Of course, these are only toy examples and they address only the computation of the forward pass. But the same ideas apply to real neural networks. The following figure shows an allocation plan for a two-layer perceptron.
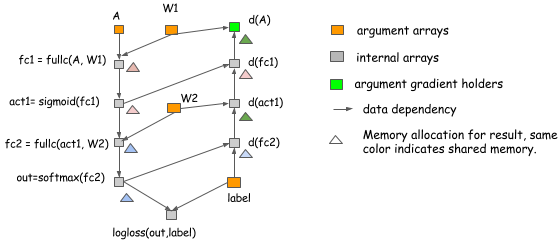
In this example:
- In-place optimization is applied when computing
act1,d(fc1),outandd(fc2). - Memory is shared between
d(act1)andd(A).
Memory Allocation Algorithm
So far, we’ve discussed general techniques for optimizing memory allocation. We’ve seen that there are traps to avoid, as demonstrated in the case of in-place memory optimization. So, how can we allocate memory correctly? This is not a new problem. For example, it is very similar to the problem with register allocation in compilers. There might be techniques that we can borrow. We’re not attempting to give a comprehensive review of techniques here, but rather to introduce some simple but useful tricks to attack the problem.
The key problem is that we need to place resources
so that they don’t conflict with each other.
More specifically, each variable has a life time
between the time it gets computed until the last time it is used.
In the case of the multi-layer perceptron,
the life time of fc1 ends after act1 get computed.

The principle is to allow memory sharing only between variables whose lifetimes don’t overlap.
There are multiple ways to do this.
You can construct the conflicting graph
with each variable as a node and link the edge
between variables with overlapping lifespans,
and then run a graph-coloring algorithm.
This likely has $O(n^2)$ complexity,
where n is the number of nodes in the graph.
This might be too costly.
Let’s consider another simple heuristic. The idea is to simulate the procedure of traversing the graph, and keep a count of future operations that depends on the node.
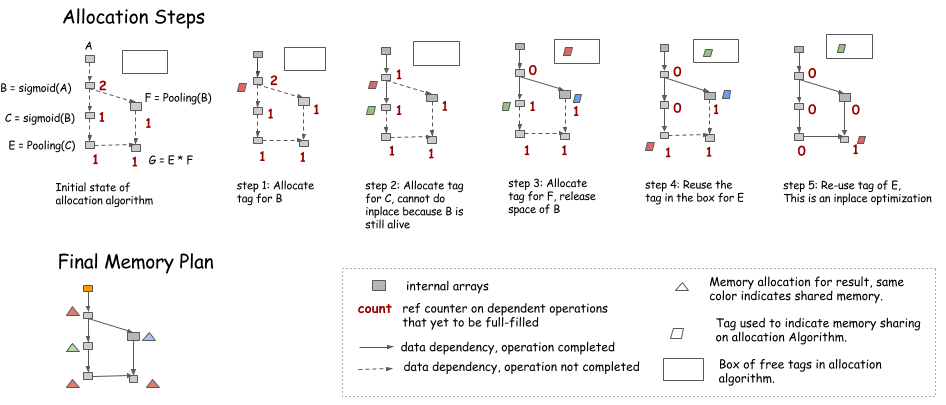
- An in-place optimization can be performed when only the current operation depends on the source (i.e.,
count==1). - Memory can be recycled into the box on the upper right corner when the
countgoes to 0. - When we need new memory, we can either get it from the box or allocate a new one.
Note: During the simulation, no memory is allocated. Instead, we keep a record of how much memory each node needs, and allocate the maximum of the shared parts in the final memory plan.
Static vs. Dynamic Allocation
The preceding strategy exactly simulates
the dynamic memory allocation procedure
in imperative languages, such as Python.
The count is the reference counter for each memory object,
and the object gets garbage collected
when the reference counter goes to 0.
In that sense,
we are simulating dynamic memory allocation once
to create a static allocation plan.
Can we simply use an imperative language
that dynamically allocates and deallocates memory?
The major difference is that static allocation is only done once, so we can afford to use more complicated algorithms. For example, we can search for memory sizes that are similar to the required memory block. The Allocation can also be made graph aware. We’ll talk about that in the next section. Dynamic allocation puts more pressure on fast memory allocation and garbage collection.
There is also one takeaway for users who want to rely on dynamic memory allocations: do not unnecessarily reference objects. For example, if we organize all of the nodes in a list and store then in a Net object, these nodes will never get dereferenced, and we gain no space. Unfortunately, this is a common way to organize code.
Memory Allocation for Parallel Operations
In the previous section, we discussed how we can simulate running the procedure for a computation graph to get a static allocation plan. However, optimizing for parallel computation presents other challenges because resource sharing and parallelization are on the two ends of a balance. Let’s look at the following two allocation plans for the same graph:
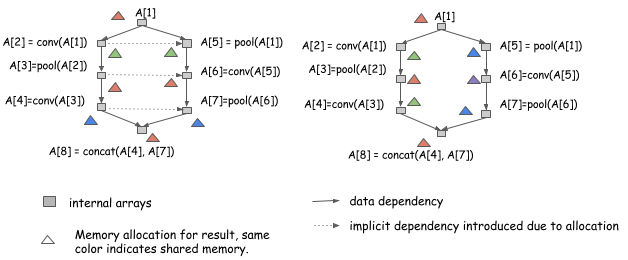
Both allocation plans are valid
if we run the computation serially,
from A[1] to A[8].
However, the allocation plan on the left
introduces additional dependencies,
which means we can’t run computation of A[2] and A[5] in parallel.
The plan on the right can.
To parallelize computation, we need to take greater care.
Be Correct and Safe First
Being correct is our first principle. This means to execute in a way that takes implicit dependency memory sharing into consideration. You can do this by adding the implicit dependency edge to the execution graph. Or, even simpler, if the execution engine is mutation aware, as described in our discussion of dependency engine design, push the operation in sequence and write to the same variable tag that represents the same memory region.
Always produce a safe memory allocation plan. This means never allocate the same memory to nodes that can be parallelized. This might not be ideal when memory reduction is more desirable, and we don’t gain too much when we can get benefit from multiple computing streams simultaneously executing on the same GPU.
Try to Allow More Parallelization
Now we can safely perform some optimizations.
The general idea is to try and encourage memory sharing between nodes that can’t be parallelized.
You can do this by creating an ancestor relationship
graph and querying it during allocation,
which costs approximately $O(n^2)$ in time to construct.
We can also use a heuristic here,
for example, color the path in the graph.
As shown in the following figure,
when you try to find the longest paths in the graph,
color them the same color and continue.
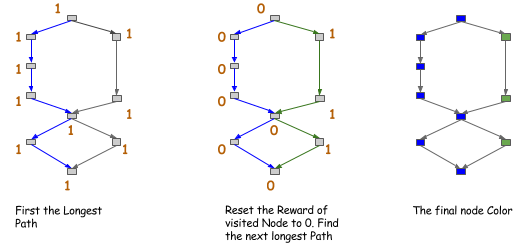
After you get the color of the node,
you allow sharing (or encourage sharing)
only between nodes of the same color.
This is a stricter version of the ancestor relationship,
but it costs only $O(n)$ of time
if you search for only the first k path.
This is by no means the only solution. More sophisticated approaches might exist:
How Much Can you Save?
We’ve discussed the techniques and algorithms you can use to squeeze memory usage for deep learning. How much can you really save by using these techniques?
On coarse-grained operation graphs that are already optimized for big operations, you can reduce memory consumption roughly by half. You can reduce memory usage even more if you are optimizing a fine-grained computation network used by symbolic libraries, such as Theano. Most of the ideas in this article inspired the design of MXNet.
Also, you will notice that memory cost, for forward pass only execution, is extremely low compared to running both forward and backward pass. This is simply because there’s more memory reuse if you run only the forward pass.
So here are two takeaways:
- Use a computation graph to allocate memory.
- For deep learning models, prediction consumes much less memory than training.
